Fractals on the Riemann Sphere

Published 2016-12-06

In order to investigate the behaviour of Newton Fractals at infinity, I've plotted Newton Fractals on the Riemann sphere. Here's an animated video of a Newton Fractal plotted on the Riemann sphere using YouTube's 360° video feature:

Since I was making videos for YouTube, I decided that I might as well animate the newton fractals by generating many newton fractals where I vary the function slightly. Since I was making a lot of fractals, which was taking a long time, I decided to do the computations on the GPU for this project. This was also my first time using the GPU.

The code I wrote to generate these videos can be found on GitHub. In general, using the GPU wasn't very difficult. I could essentially write the function I wanted to run using normal C++ code, so I won't go into further details about this here. You can read the code yourself if you want.

There are, however, two things, that I do want to explain: How one creates 360° videos for YouTube, and how I use dual numbers to make changing the function easier.

Dual numbers

Having to define both the function and its derivative sucks. Luckily we can get away with only the function by using dual numbers.

In dual numbers, we add a new value ε to the number system. This new value satisfies the identity ε² = 0, similar to how the imaginary unit is introduced for complex numbers. This is cool because the Taylor expansion of f(x+ε) around x can be written in following form:

f(x+ε) = f(x) + fʹ(x)·ε + O(x²)·ε²

This means every term beside the first two are multiplied by ε², which is zero, allowing us to write f(x+ε) simply as f(x) + fʹ(x)·ε. More generally we have f(x+aε) = f(x) + afʹ(x)·ε.

Using these properties, you can type the function once in your program, and when you evaluate the function at the dual number x+ε, you obtain the value and derivative at that point. My implementation of these numbers can be found in the GitHub repository.

360° videos

In order for a 360° video to be displayed properly on YouTube, it has to be encoded using an equirectangular projection. This means that the x coordinate is mapped to the longitude, and the y coordinate is mapped to the latitude. In other words, a vertical line in the image corresponds to a straight line from the top of the sphere to the bottom of the sphere, and each horizontal line corresponds to a horizontal ring in the sphere. This means the 'resolution' of the image will be higher at the top and bottom than in the middle.

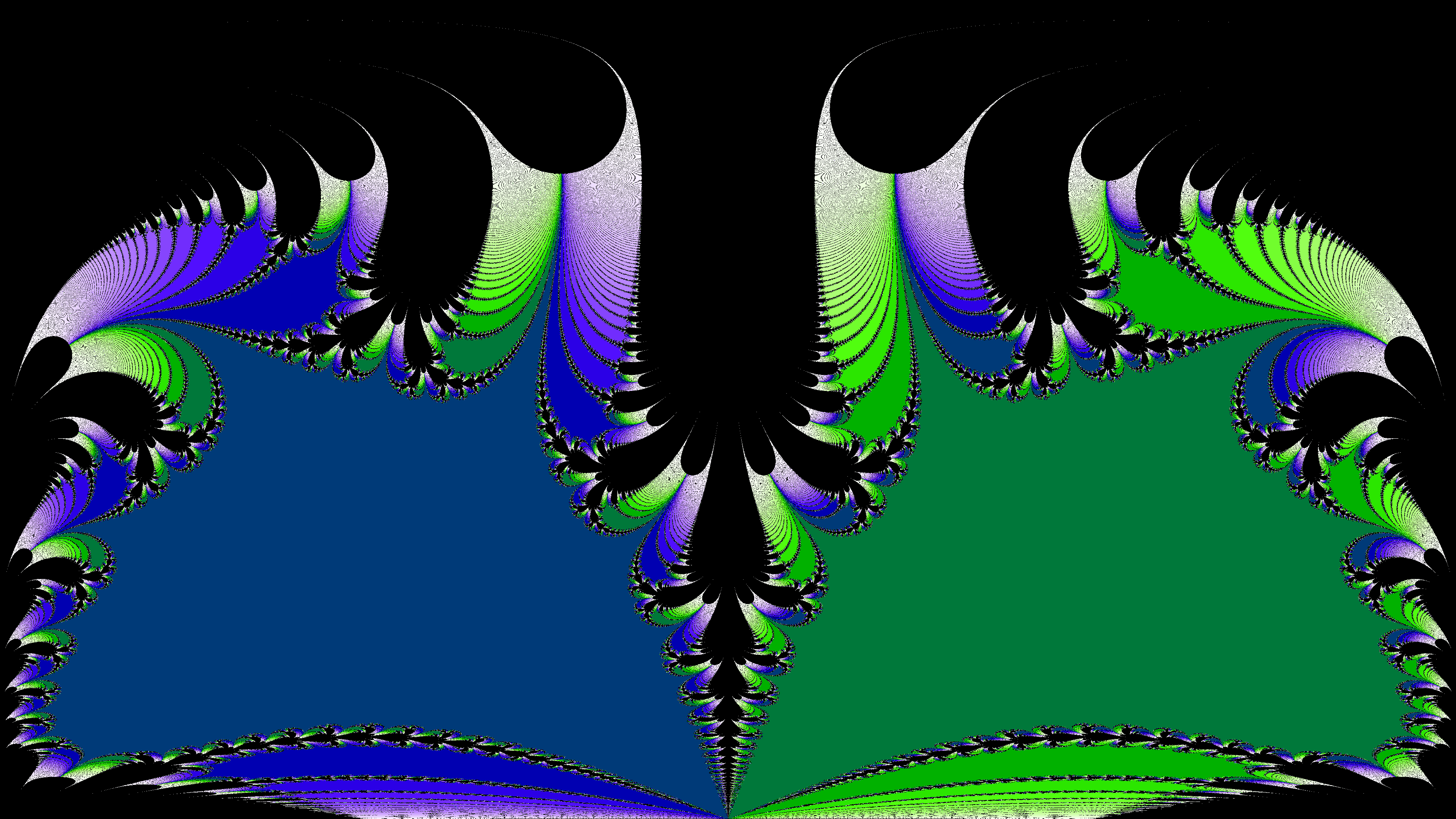
$A newton fractal on the Riemann sphere shown using an equirectangular projection$

A newton fractal on the Riemann sphere shown using an equirectangular projection.

Since I was making newton fractals, I needed to map the pixels to complex numbers. On the Riemann sphere, one can compute the complex number corresponding to a specific longitude and latitude using the formula

z = tan(φ)·e^iλ,

where φ is the latitude, and λ is the longitude. Then all there is left is to linearly scale the parameters to match the resolution of the image.

Marking video files as spherical

The last important bit is how one can tell YouTube that the video is spherical, and not flat. This is pretty easy using the Python tool “spatial media”. The commands I used to make my video files spherical are the following:

$ git clone --depth=1 https://github.com/google/spatial-media spatial-media
$ python2 ./spatial-media/spatialmedia/__main__.py -i flat-video.mp4 spherical-video.mp4

Depending on your setup you might need to run it as just python, instead of python2 like I did.